《横截相交的不变流形所揭示的三维磁拓扑混沌本性》

Author: Wenyin Wei (魏wèi ~ 文wén 崟yín) and Yunfeng Liang (梁liáng ~ 云yún 峰fēng)
Conference: The 48th European Conference on Plasma Physics (2022) EPS48, 欧洲物理年会第 48 届等离子体分会
Poster Number: P5b.110
Time: July 1st 2022, Friday, 3:30-4:30 p.m. (UTC+2) / 2022年7月1日北京时间周五晚上9:30-10:30 (UTC+8), Poster Session 2
Schedule: see https://indico.fusenet.eu/event/28/sessions/64/
EPS poster link: https://epsplasma2022online.nl/poster/the-chaotic-nature-of-three-dimensional-magnetic-topology-revealed-by-transversely-intersecting-invariant-manifolds/ (EPS48 account required)
Abstract pdf: here is the download link.
Poster pdf: please send an email to Wenyin to ask for it: wenyin.wei@ipp.ac.cn .

Abstract:
Although adopted by Grad-Shafranov equation, EFIT, VMEC, etc., the nested closed flux surface assumption does not necessarily hold when the axial symmetry of magnetic field is absent. An abundant amount of research has focused on how to stimulate a chaotic field layer at the plasma boundary to mitigate destructive type-I edge localized modes. With regard to the influence of topology change on the scrape-off layer, a spiral ribbon-like pattern of heat deposition has also been reported and investigated in experiments. Based on the theory of dynamical system and chaos, we formalized relevant notions concerning magnetic topology and revealed the global structure of three-dimensional magnetic field. The invariant manifold growth formula in cylindrical coordinates is deduced and essential to determine the chaotic field regions (used to be called stochastic field), which induce a mixing effect inside plasma. It is proposed that the well-known notion of the last closed flux surface is substituted by more accurate invariant manifolds of the outmost hyperbolic cycle(s). The transverse intersection of invariant manifolds is a signature of chaos, indicating the intrinsic unpredictability (of field line tracing) in the long run. Having acquired the analytical form of invariant manifolds, we further regard the whole magnetic field as a functional argument of Poincaré map and utilize the functional (Fréchet) derivative from functional analysis to obtain the X/O-point shift under perturbation (δB) formula. Undoubtedly, the most important perturbation field is the derivative of magnetic field itself w.r.t. time, i.e. ∂B/∂t, giving the shift velocity of X/O-points when δB is substituted for ∂B/∂t in the formula above.

  In conclusion, a systematic analytic theory of three-dimensional magnetic fields has been established to facilitate comprehending the field structure and to provide guidance on control.

摘要:
虽然嵌套闭合磁面假设在 Grad-Shafranov 方程、EFIT、VMEC 等中都被视作成立，但磁场非轴对称时这一假设可能是不成立的。已有的许多研究试图激发出等离子体边界处的混沌场层以缓解破坏性的 I 型边界局域模（ELM）。而拓扑变化对刮削层的影响，实验中亦报道了偏滤器上的螺旋带状热沉积并进行了研究。基于动力系统和混沌理论，我们对有关磁拓扑的相关概念进行了形式化，并揭示三维磁场的全局结构。本工作中推导了柱坐标中的不变流形生长公式，其对于混沌场区域（过去称为随机场）的确定起到关键作用，混沌场会在等离子体内部起到一定的混匀作用。我们建议用更准确的 最外鞍环（或称双曲环）的不变流形（the invariant manifolds of the outmost hyperbolic cycle(s)） 代替过去广为使用的最外闭合磁面（last closed flux surface, LCFS）。横截相交的不变流形是混沌的标志，表征（场线追踪的）长期行为具有本征的不可预测性。在获得了不变流形的解析式后，我们进一步将整个磁场视为庞加莱映射的一个函数参数，并利用泛函分析中的泛函（Fréchet）导数获得 X/O 点在扰动下 (δB) 的偏移 公式。最重要的扰动场毫无疑问是磁场本身对于时间的导数，即 ∂B/∂t；如果将这一扰动场代入上式中的 δB，我们就得到 X/O 点的偏移速度 公式。

  总而言之，本工作着手建立了系统的三维磁场的解析理论，有助于理解场的结构并为磁拓扑的控制提供指导。

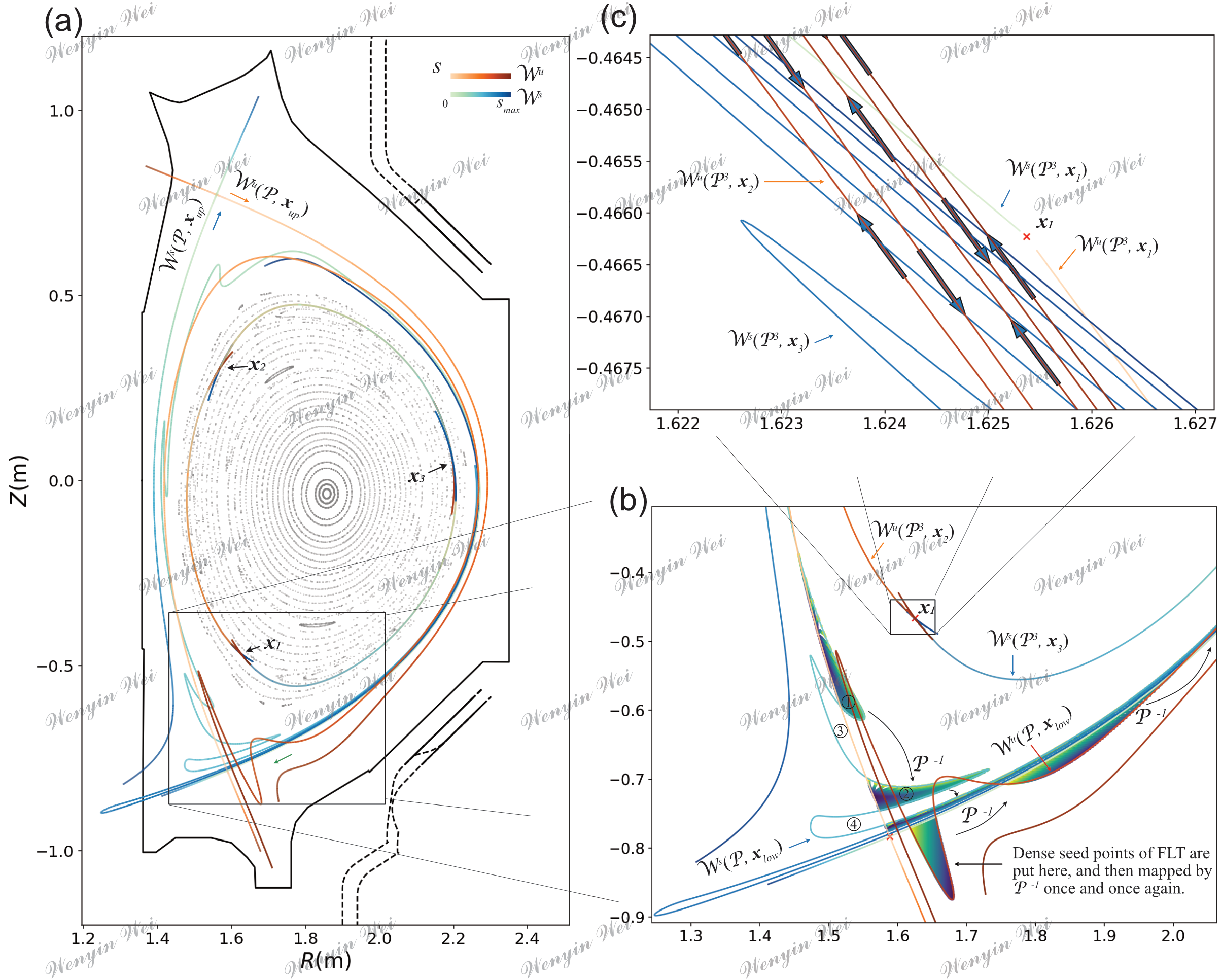
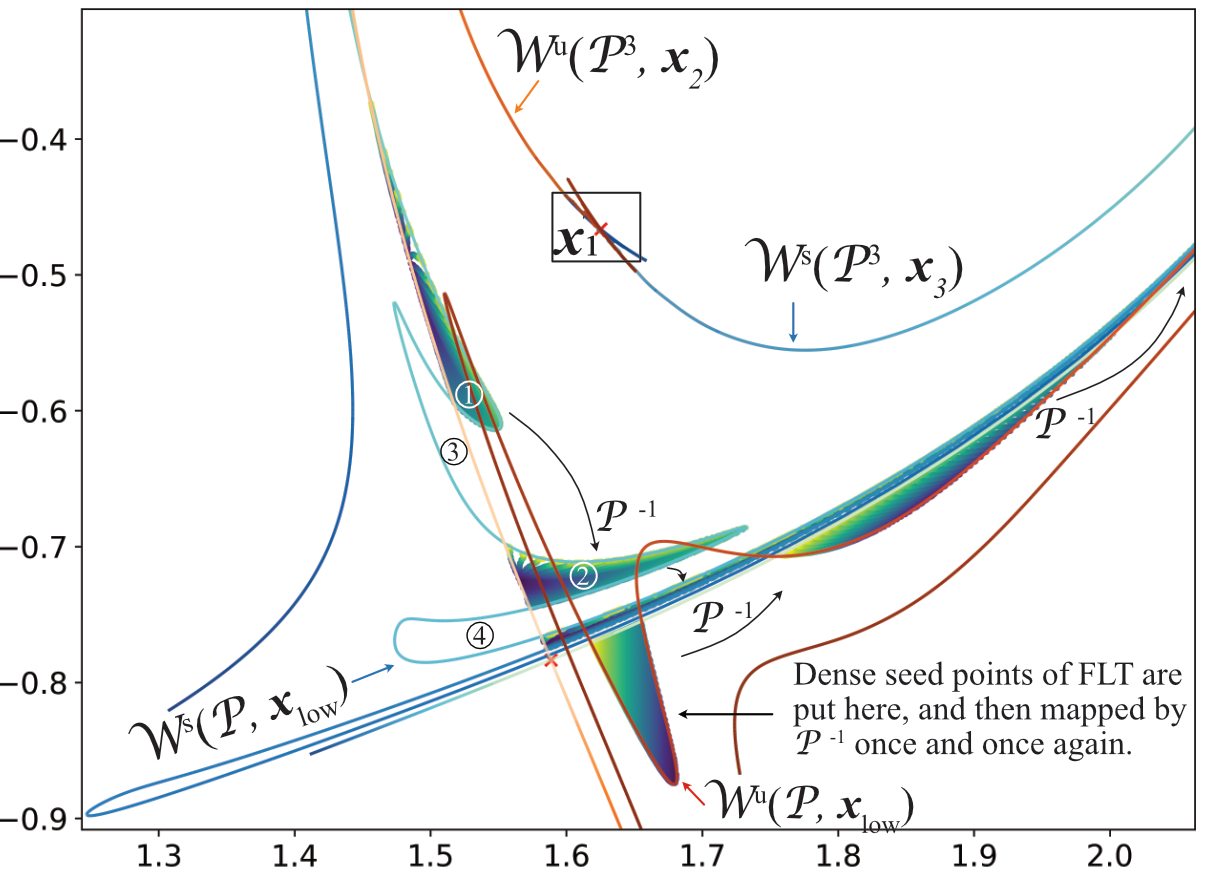
Fig 1. (a) EAST #103950 at 3500ms Poincaré plot (EFIT+RMP vacuum) and the manifolds of the outmost saddle cycles and q=m/n=3/1 X-cycle. (b) Enlarged view of (a) near the lower X-point. Dense scatter points with distinctive color (so dense that they look like cloud) are presented to indicate how the regions are connected by field lines. (c) Enlarged view of (b) near the X-point x_{1} of the q=m/n=3/1 island chain