《不变流形生长公式及其在磁约束聚变中的应用》

Tip for physicists: Colloquially, the stable manifold is the set of points that will flow into an invariant set at an exponential rate under the dynamical system; the unstable manifold is the set of points that flowed from an invariant set at an exponential rate under the dynamical system. A set is invariant if, once a point comes in this set, its trajectory will never go out of this set. The set of points on an X-cycle is an invariant set; its corresponding stable and unstable manifolds are also invariant sets. The term invariant manifold in our title refers to the stable and unstable manifolds of an X-cycle.
通俗地说稳定流形是指在一给定向量场的流下将以指数率汇入一不变集的点的集合；不稳定流形是指在一给定向量场的流下从一不变集以指数率流出的点的集合。不变是指一旦某个点落到这一集合中，它的流就不会流出该集合，故称不变。X 环上点的集合是一不变集，X 环对应的稳定和不稳定流形也是一不变集，我们的题目不变流形指的就是鞍环的稳定和不稳定流形。

Author: Wenyin Wei (魏wèi ~ 文wén 崟yín) and Yunfeng Liang (梁liáng ~ 云yún 峰fēng)
Type: Paper
Abstract:
A spiral ribbon-like pattern of heat deposition has been reported and investigated in the past, of which the field structure is essential to study how to expand the wet area of heat flux to reduce the tolerance-to-heat demand for materials at the divertor in a magnetically confined fusion device. The relevant notions concerning magnetic topology are formalized in this paper to utilize knowledge from dynamical system research. Of great importance to comprehending the topology of general 3D vector fields are cycles and the invariant manifolds grown from saddle cycles, which are analyzed in detail. How the Jacobian of Poincaré map evolves along a cycle is presented. Grown in the directions of the Jacobian eigenvectors at the beginning, the invariant manifolds of saddle cycles are essential to determine the chaotic field regions, which induce a mixing effect inside the plasma. With regard to three-dimensional continuous-time dynamical systems, the governing equation of invariant manifolds in cylindrical coordinates is deduced.

过去的研究中已发现偏滤器上螺旋条带状的热负荷分布，三维磁场的结构对如何增大热负荷湿区以降低偏滤器材料的耐热要求至为关键。本文将磁拓扑相关的概念形式化以利用动力系统中的知识。对于一般三维向量场拓扑的理解，环和鞍环上生长出的不变流形十分重要，本文对其有详细分析。Poincaré 映射的 Jacobian 在环上如何演化，文中给出其公式。鞍环的不变流形从 Poincaré 映射的 Jacobian 矩阵的特征向量上长出，它们对混沌场区的确定十分重要，混沌场会在等离子体中造成一定的混合效应。就三维连续时间动力系统，本文推导得到柱坐标中不变流形的生长公式。

Links:

• Journal: Plasma Science and Technology, https://iopscience.iop.org/article/10.1088/2058-6272/accbf5/meta
• Chinaxiv: https://chinaxiv.org/abs/202211.00236
• arXiv: We had struggled with arXiv's Tex engine but still failed to generate a satisfactory pdf by arXiv's online engine. And it does not support xelatex, which is a common solution for typing CJK (Chinese, Japanese, Korean) characters.
• ResearchGate (usually latest because no platform check): https://www.researchgate.net/publication/365632460_Invariant_manifold_growth_formula_in_cylindrical_coordinates_and_its_application_for_magnetically_confined_fusion

Figures in the paper:

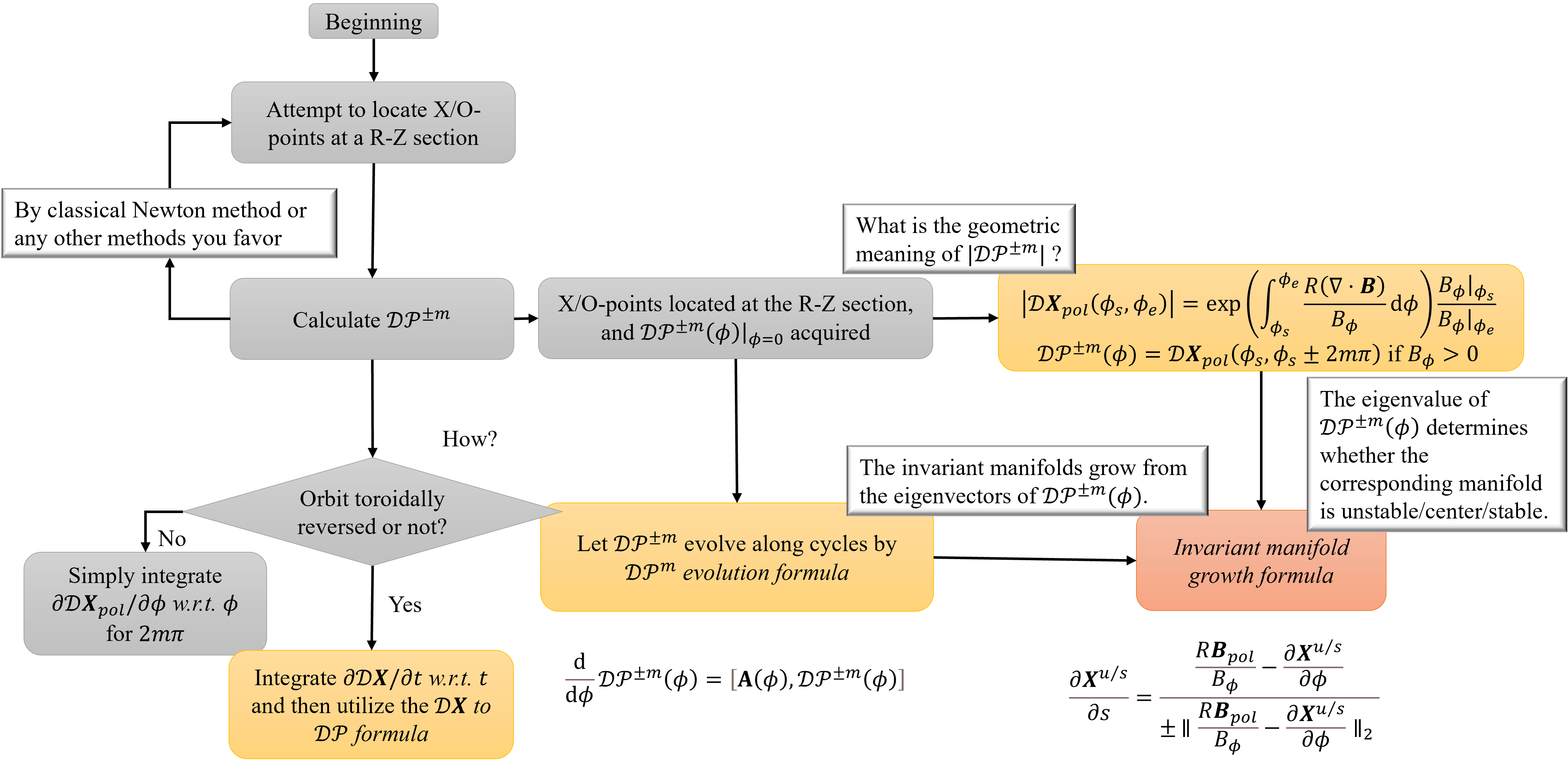
Fig. Thought process map of our paper, where the grey boxes are not new.

Fig. A demonstration model of what we call Möbiusian cycle.

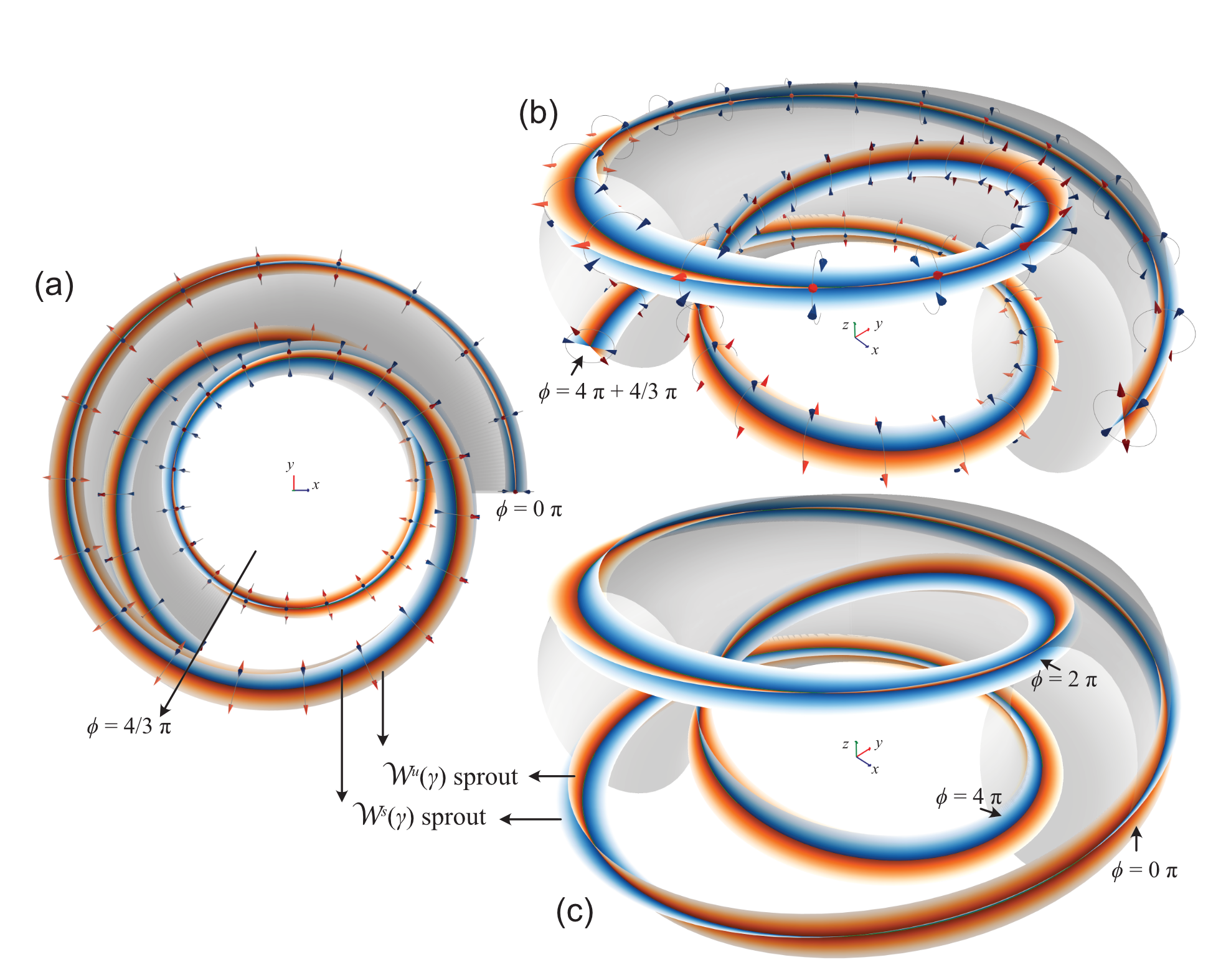
Fig. A demonstration model of dummy X-cycle.

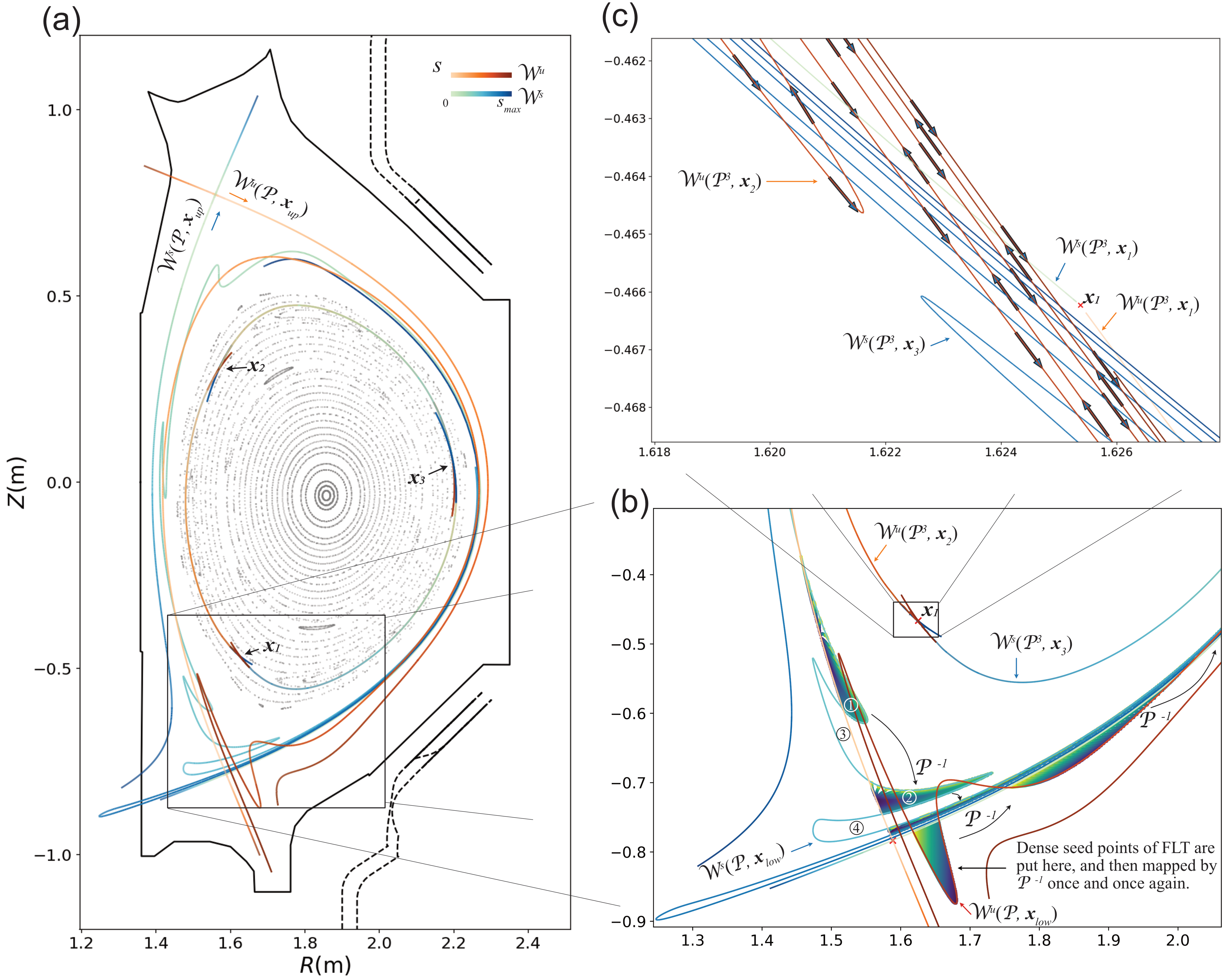
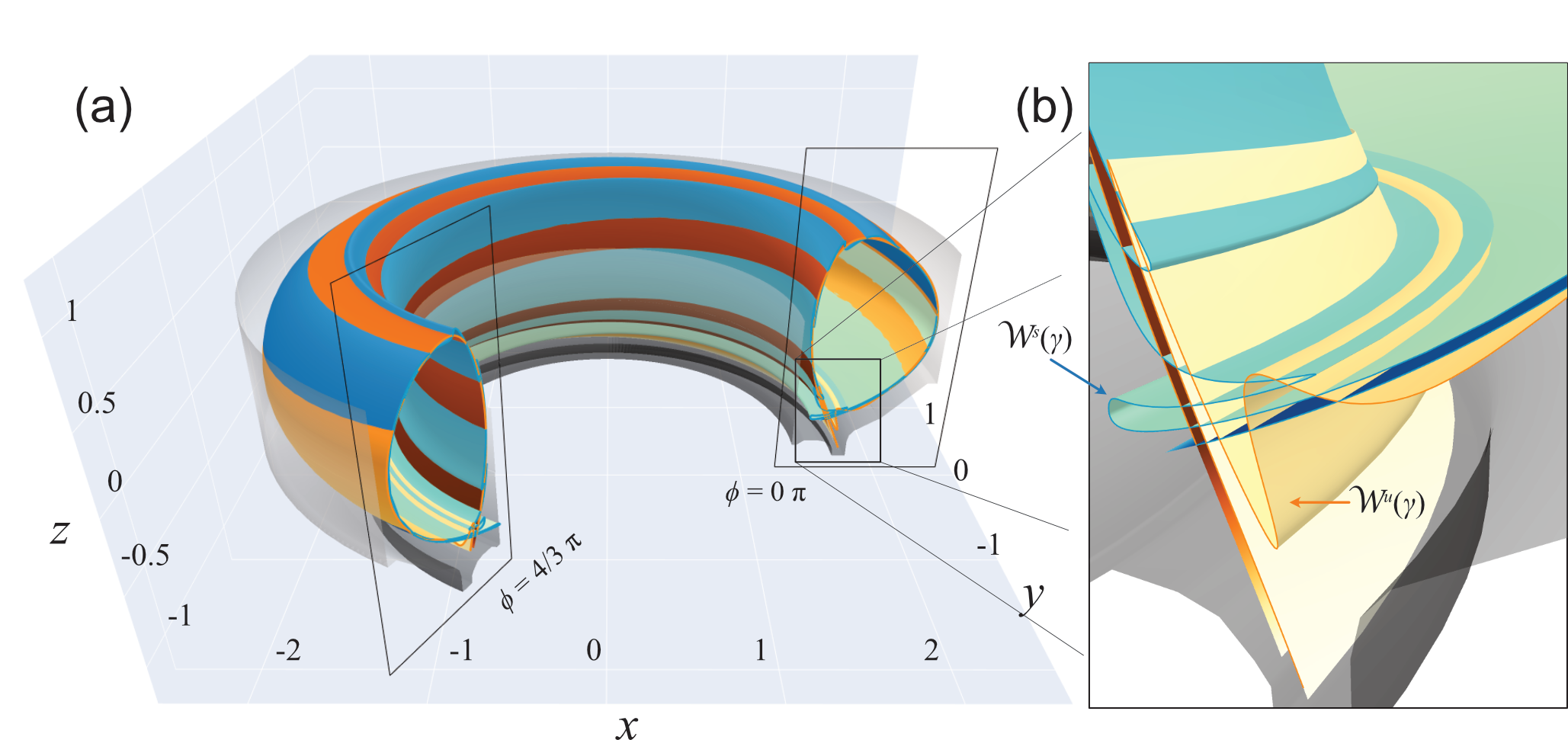
Figs. A realistic demonstration of invariant manifolds in a fusion experiment EAST #103950 3500ms, EFIT+RMP vacuum.

Invited talk

应等离子体所伍兴权老师的邀请，暂定于周四下午两点至四点作公开报告。

报告题目：
《不变流形生长公式及其在磁约束聚变中的应用》
Invariant manifold growth formula in cylindrical coordinates and its application for magnetically confined fusion
报告语言：幻灯片中英双语，口头语言中文；Slides in both English and Chinese, oral in Chinese。
报告时间：2022 年 11 月 24 日, November 24, 14:00-16:00 p.m.
报告 PDF：here is the download link.
报告内容：
过去的研究中已发现偏滤器上螺旋条带状的热负荷分布，三维磁场的结构对如何增大热负荷湿区以降低偏滤器材料的耐热要求至为关键。混沌存在于三维或三维以上的连续时间动力系统中，使得三维磁场呈现出比轴对称磁场更为复杂的结构，嵌套闭合磁面假设不一定成立。本次报告首先会简要介绍以往磁约束聚变研究中相关方面的模拟和实验研究结果、传统的径向磁扰动的磁谱分析方法，以及数学界的一些经典定理，如 KAM、Poincaré-Birkhoff、Poincaré-Hopf 等定理。对于一般三维向量场（一般指无需散度为零）的拓扑，环和鞍环上生长出的不变流形尤为重要，我们给出不变流形生长公式，该部分仅需要多元微积分的知识。鞍环的不变流形从 Poincaré 映射的 Jacobian 矩阵的特征向量上长出，即这两个特征向量是流形生长公式的初始条件。为避免对每个R-Z截面都做一次不必要的积分以求得该 Jacobian，我们给出其在环上的演化公式。对任意有限维的自治连续时间动力系统中环上的 Jacobian 演化，该公式也可应用。E×B 偏移无关于粒子速度，如要考虑之，可直接代入我们的公式中将一般向量场 B 替换作 B+E×B/B^2。各公式的数值化实现将也会在报告中展示，解析与现实数值的不变流形的例子兼而有之。如何增大边界等离子体磁力线连接长度、提高辐射损失以实现脱靶，是未来有希望的研究方向。
本次报告不会过多涉及推导。

本次报告是我们在第四十八届欧洲物理年会等离子体分会上的海报《横截相交的不变流形所揭示的三维磁拓扑混沌本性》The chaotic nature of 3D magnetic topology revealed by transversely intersecting invariant manifolds 的前半部分，即海报的左侧栏部分。右侧栏的理论则用于刻画一般三维向量场在扰动场的作用下其中的环会如何偏移，本报告中仅一笔带过。